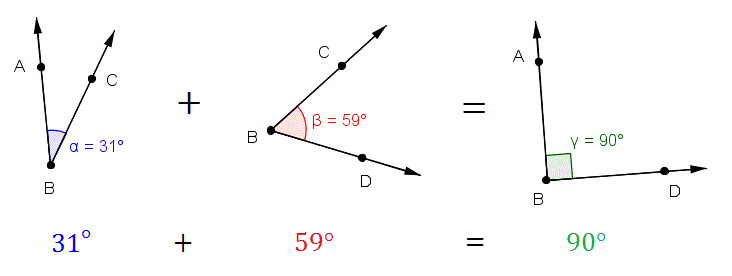
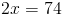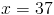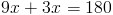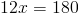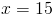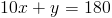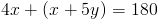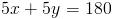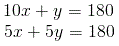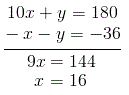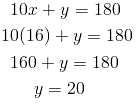Parallel and Perpendicular Lines
Now that we have a better understanding of lines and angles, we are ready to begin applying some of these concepts onto the Caresian coordinate plane. We will use our previous knowledge of slopes and algebraic equations to learn about parallel and perpendicular lines in the coordinate plane.
Although the coordinate plane is used extensively in the study of algebra, it is very useful in geometry as well. In algebra, when you study slope, essentially what you are dealing with is angles. More specifically, the slope of a line is the measure of an angle of a line from a perfectly horizontal line (or the x-axis). This concept is illustrated below.This goes to show that different areas of mathematics are connected and consistent with each other.
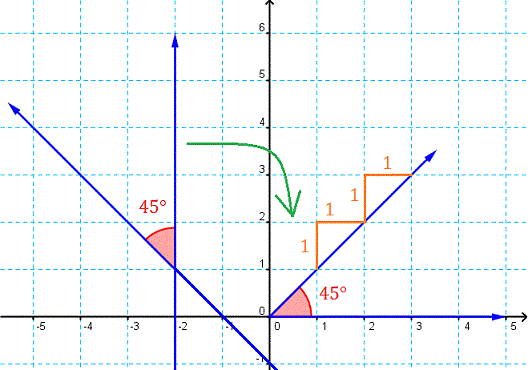
You can take an angle formed by two lines and place one of the lines on the x-axis to see a relationship between angles and slopes.
Parallel Lines
Recall that two lines in a plane that never intersect are called parallel lines. Working with parallel lines in the coordinate plane is fairly straightforward. The reason for this is because the slope of a line is essentially the measure of an angle of a line from a perfectly horizontal line (or the x-axis). Thus, in the coordinate plane, if we want two different lines to never intersect, we simply apply the same slopes to them.
Let's take a look at the following equations:
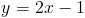
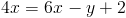
How do we determine if these lines are parallel or if they intersect at some point?
First, it will help to put both equations in slope-intercept form. The first equation is already of this form so we do not need to change it. The second equation, however, needs to be manipulated. Let's work it out:
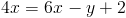
Now, we add y to both sides of the equation to get
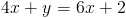
Subtracting 4x from both sides of the equation gives
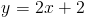
Now, if we look at both equations, we notice that they both have slopes of 2. Since both lines "rise" two units for every one unit they "run," they will never intersect. Thus, they are parallel lines. The graph of these equations is shown below.
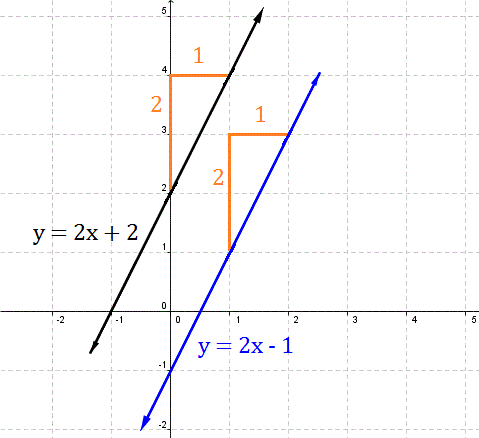
We now see that the two lines are parallel. But how many more lines can we find that are parallel to them? The answer is infinitely many. As long as the lines have slopes of 2, they will never intersect.
Now let's try a type of problem that requires a bit more work.
Example 1
Find the equation of a line that passes through the point (3, 1) and is parallel to the line
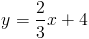
In order to solve this kind of problem, we will need to keep in mind that parallel lines have the same slope. We will also have to utilize what we know about equations in slope-intercept form.
In slope-intercept form, x and y are variables that will change, so we do not determine an exact value for them. All that is left to solve for are m and b, where m is our slope and b is the y-intercept of our line. Recall that parallel lines have the same slope, so m = 2/3 in this example. We have:
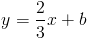
We only need to solve for b now. We do this by plugging in the given point, (3, 1), that lies on our line. This method is shown below.
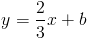
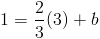
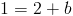
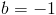
Since we determined that m = 2/3 and that b = -1, we can plug these values straight into our slope-intercept formula. This yields
We can take a look at the graph of these lines to see that this line is indeed parallel to the given line and that it passes through (3, 1).
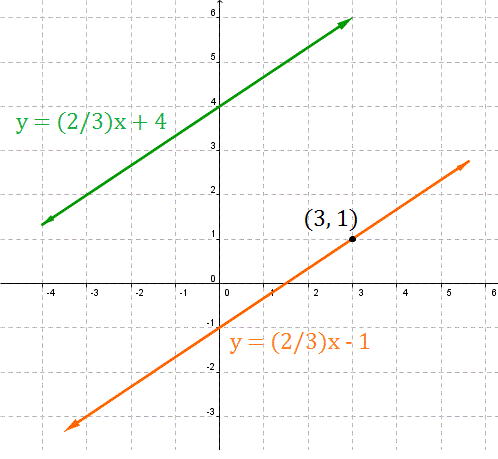
Perpendicular Lines
Pairs of lines that intersect each other at right angles are called perpendicular lines. The symbol that represents perpendicularity between two lines is ?. Thus, if line AB meets line CD at a 90° angle, we express it mathematically as  . Perpendicular lines are shown below.
. Perpendicular lines are shown below.
 . Perpendicular lines are shown below.
. Perpendicular lines are shown below.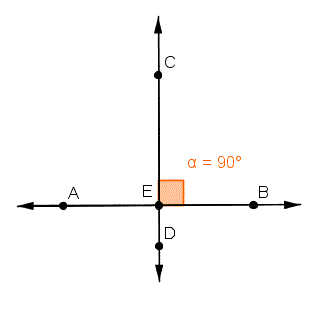
The intersection of line AB with line CD forms a 90° angle
There is also a way of determining if two lines are perpendicular to each other in the coordinate plane. While parallel lines have the same slope, lines that are perpendicular to each other have opposite reciprocal slopes. We can determine perpendicularity just by looking at the equations of lines just as we did with parallel lines. For instance, consider the line
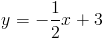
If we want to find the equation of a line that is perpendicular to the given line we just need to follow two simple steps.
(1) Take the reciprocal (or flip the fraction) of the slope:
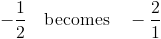
(2) Make it the opposite sign:
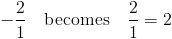
Any line with a slope of 2 will be perpendicular to the given line. Since there are infinitely many lines with this slope, there are infinitely many lines perpendicular to the given line.
Note: It is a common mistake to only take the reciprocal of a line's slope and forget about taking the opposite of the slope. Why doesn't this work? If we did not take the opposite sign of the slope, we would have two lines with either positive or negative slopes. This would make it impossible for the lines to ever meet at a 90°. In short, remember that perpendicular lines have opposite reciprocal slopes.
Let's try another example.
Example 2
Find the equation of the line that passes through the point (8, 1) and is perpendicular to the line
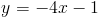
Similar to the Example 1, we first identify what the slope of our equation should be. The slope of the line we are given is -4, so we perform the following steps to find the slope:
(1) Take the reciprocal of the slope:
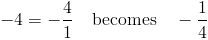
(2) Make it the opposite sign:
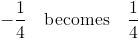
Now we have
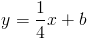
So, we plug in the the x and y values of the point we were given to get
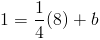
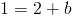
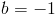
We now plug in the m and b values we have found, so the equation of our line is
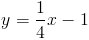
We see that there does indeed exist a right angle at the intersection of the two lines in the figure shown below.

The lines are perpendicular to each other